Types of Graph
Here's a detailed explanation of the different types of graphs in Data Structures and Algorithms (DSA), along with examples.
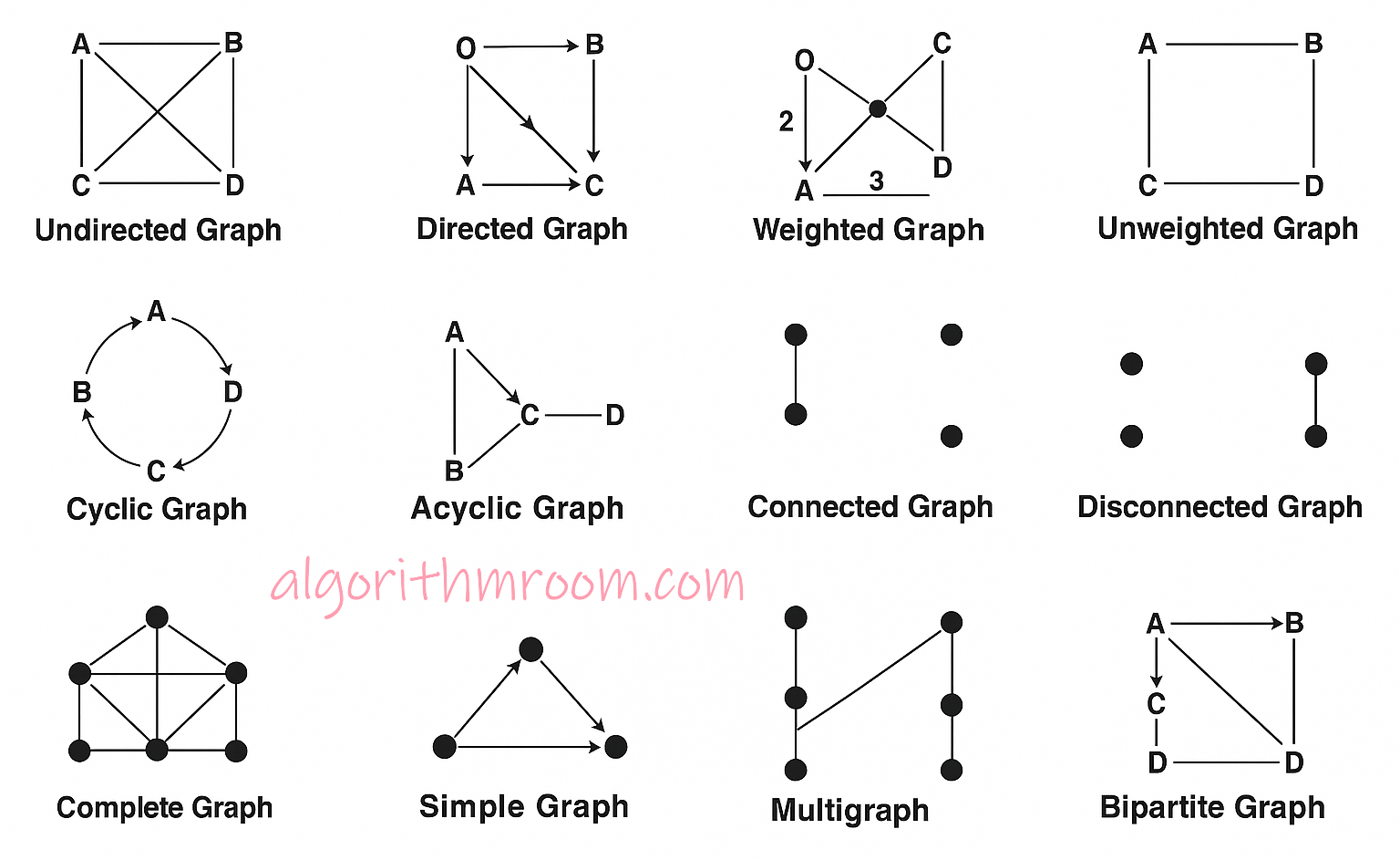
Types of Graph
- Directed Graph
- Undirected Graph
- Complete Graph
- Regular Graph
- Cyclic Graph
- Acyclic Graph
- Weighted Graph
- Unweighted
- Connected
- Disconnected
- Simple
- Multigraph
- Bipartite
- Tree
Directed Graph: (Diagraph)
A directed graph is graph, i.e., a set of objects (called vertices or nodes) that are connected together, where all the edges are directed from one vertex to another.
A directed graph is sometimes called a digraph or a directed network.
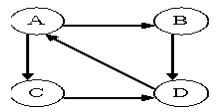
Example
- Twitter (follow relationship)
- Web Page links (A links to B doesn't mean B links back)
- Workflow/task dependencies
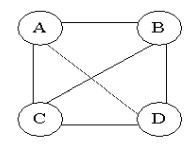
Undirected Graph: (Bidirectional)
An undirected graph is graph, i.e., a set of objects (called vertices or nodes) that are connected together, where all the edges are bidirectional.
An undirected graph is sometimes called an undirected network. In contrast, a graph where the edges point in a direction is called a directed graph.
Example
- Social networks (friendship)
- Road maps with two-way streets
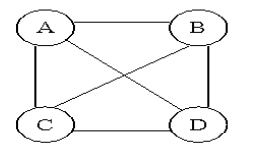
Complete Graph
A graph in which any V node is adjacent to all other nodes present in the graph is known as a complete graph.
An undirected graph contains the edges that are equal to edges = n(n-1)/2 where n is the number of vertices present in the graph.
Example
- Theoretical models
- Network design to guarantee maximum connectivity
Regular Graph
Regular graph is the graph in which nodes are adjacent to each other, i.e., each node is accessible from any other node.

Cycle Graph
A graph that contains one or more cycles, i.e., a path where the start and end vertices are the same, with at least one intermediate vertex.
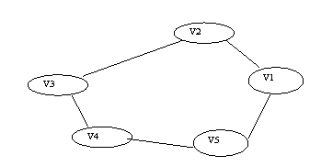
Example
- Circular dependencies in tasks
- Infinite loops in state machines (to be detected)
Acyclic Graph
A graph with no cycles.
- In undirected acyclic graphs, you get a Tree.
- In directed acyclic graphs (DAGs), the graph flows in one direction without forming a loop.
Example
- Task scheduling
- Compilation order
- Data processing pipelines
Weighted Graph
A graph is said to be weighted if there are some non negative value assigned to each edges of the graph.
The value is equal to the length between two vertices. Weighted graph is also called a network.
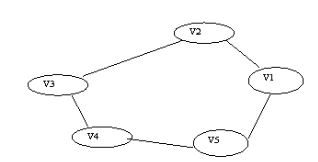
Example
- GPS or Map applications (distance/time)
- Network routing (bandwidth/cost)
- Airline networks (flight cost or duration)
Connected Graph
An undirected graph is connected if there is at least one path between every pair of vertices.
Example
- Network topology validation
- Ensuring all users are reachable
Disconnected Graph
An undirected graph where some vertices are not reachable from others.
Example
- Fault detection in network
- Identifying isolated subgroups
Simple Graph
A graph with:
- No self-loops
- No multiple edges between the same pair of vertices
Example
- Most standard graph problems assume simple graphs
Multigraph
A graph that allows multiple edges between the same pair of vertices (also called parallel edges).
Example
- Transportation networks (multiple roads between two cities)
- Packet routing paths
Directed Acyclic Graph (DAG)
A directed graph that has no cycles.
You cannot return to the same vertex once you move forward.
Example
- Topological sorting
- Task scheduling with dependencies
- Build systems (e.g., Makefile)
Bipartite Graph
A graph whose vertices can be divided into two sets U and V, such that every edge connects a vertex from U to one in V.
Example
- Matching problems (job assignment, pairing)
- Network flow
- Recommendation systems
Tree (as a special graph)
A tree is a connected acyclic undirected graph.
Properties:
- Has
n−1edges fornvertices - Only one path between any two vertices
Example
- File systems
- Hierarchical data structures (organization charts, family trees)
Summary Table
| Type | Key Property | Use-Case Example |
|---|---|---|
| Undirected | Mutual connections | Social networks |
| Directed | One-way connections | Web links |
| Weighted | Costs on edges | Maps, routing |
| Unweighted | No weights | Friend networks |
| Cyclic | Has loops | Deadlock detection |
| Acyclic | No loops | Task scheduling |
| Connected | Every node reachable | Internet topology |
| Disconnected | Some nodes not reachable | Faulty networks |
| Complete | All pairs connected | Theoretical models |
| Simple | No parallel edges or loops | Standard graphs |
| Multigraph | Multiple edges allowed | Transport systems |
| DAG | Directed and acyclic | Compiler design |
| Bipartite | Two disjoint sets connected | Job matching |
| Tree | Connected acyclic graph | File systems |
