Kruskal's Algorithm
Kruskal’s Algorithm is a greedy algorithm used to find the Minimum Spanning Tree (MST) of a connected, undirected, weighted graph.
A Minimum Spanning Tree is a subset of edges that:
- Connects all the vertices,
- Has no cycles,
- Has the minimum possible total edge weight.
How Kruskal’s Algorithm Works?
- Sort Edges by Weight (Ascending Order)
- Initialize Disjoint Sets for Vertices
- Start Adding Edges (Without Creating Cycles)
Example: Kruskal's Algorithm
Construct the minimal spanning tree for the graph shown below:

Step 1: Sort Edges by Weight (Ascending Order)
| Cost | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 | 55 |
| Edge | (1, 2) | (3, 6) | (4, 6) | (2, 6) | (1, 4) | (3, 5) | (2, 5) | (1, 5) | (2, 3) | (5, 6) |
Step 2: Initialize Disjoint Sets for Vertices
Each vertex is in its own set.
{1} {2} {3} {4} {5} {6}We will keep merging sets as we add edges to the MST.
Step 3: Start Adding Edges (Without Creating Cycles)
The stages in Kruskal’s algorithm for minimal spanning tree is as follows:
| Edge | Cost | Stages in Kruskal's Algorithm | Remarks |
| (1, 2) | 10 | 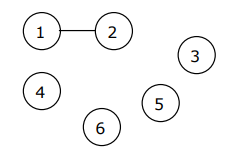 | The edge between vertices 1 and 2 is the first edge selected. It is included in the spanning tree |
| (3, 6) | 15 | 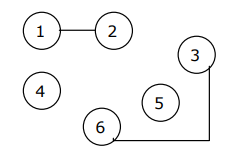 | Next, the edge between vertices 3 and 6 is selected and included in the tree. |
| (4, 6) | 20 | 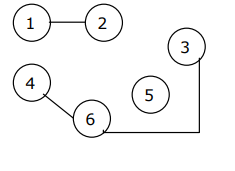 | The edge between vertices 4 and 6 is next included in the tree. |
| (2, 6) | 25 |  | The edge between vertices 2 and 6 is considered next and included in the tree. |
| (1, 4) | 30 | Reject | The edge between the vertices 1 and 4 is discarded as its inclusion creates a cycle. |
| (3, 5) | 35 |  | Finally, the edge between vertices 3 and 5 is considered and included in the tree built. This completes the tree. The cost of the minimal spanning tree is 105. |
Algorithm for Kruskal’s Algorithm
Step 1: Represent the graph as a list of all edges with their weights.
Step 2: Sort all the edges in non-decreasing order of their weights.
Step 3: Create a disjoint set (Union-Find) for all vertices to keep track of connected components.
Step 4: Initialize an empty set or list to store the edges of the Minimum Spanning Tree (MST).
Step 5: Iterate over the sorted edge list:
- For each edge (u, v):
- Use
Findto check the parent (or root) ofuandv. - If they belong to different sets:
- Add the edge to the MST.
- Use
Unionto merge the sets ofuandv.
- Use
- If they belong to the same set, skip the edge (it would form a cycle).
Step 6: Stop when you have (V – 1) edges in the MST, where V is the number of vertices.
Step 7: The edges you added form the Minimum Spanning Tree.
1. Make the tree T empty.
2. Repeat the steps 3, 4 and 5 as long as T contains less than n - 1 edges and E is
not empty otherwise, proceed to step 6.
3. Choose an edge (v, w) from E of lowest cost.
4. Delete (v, w) from E.
5. If (v, w) does not create a cycle in T
then Add (v, w) to T
else discard (v, w)
6. If T contains fewer than n - 1 edges then print no spanning tree. Union-Find (Cycle Detection)
We use the Union-Find algorithm with Path Compression and Union by Rank to detect whether two nodes are already connected (i.e., in the same set).
Operations:
Find(u): Returns the parent of u (with path compression).Union(u, v): Connects the sets of u and v (smaller ranked tree under larger one).
This helps avoid adding edges that form cycles.
Time Complexity of Kruskal's Algorithm
| Step | Time |
|---|---|
| Sorting Edges | O(E log E) |
| Union-Find Operations | O(E α(V)) |
| Total Time | O(E log E) (or O(E log V)) |
Advantages of Kruskal's Algorithm
- Efficient for sparse graphs.
- Conceptually simple.
- Does not require adjacency matrix just a list of edges.
Disadvantages of Kruskal's Algorithm
- Requires sorting of edges (costly for dense graphs).
- Slower than Prim's in dense graphs with adjacency matrix.
Applications of Kruskal's Algorithm
- Network Design: Designing minimum-cost wiring/cabling.
- Civil Engineering: Building road/railway systems with minimal cost.
- Clustering Algorithms: In ML and computer vision.
- Approximation algorithms: For NP-hard problems like TSP.
Numerical Questions for Kruskal’s Algorithm
Here are some numerical questions based on Kruskal’s Algorithm for practice, designed to help students understand sorting edges, applying Union-Find, and forming a Minimum Spanning Tree (MST).
Question 1
Given the following graph:

Task:
- Draw the MST using Kruskal’s Algorithm.
- Show sorted edges, steps for Union-Find, and total weight of MST.
Question 2
Graph:
| Edge | Weight |
|---|---|
| 1–2 | 4 |
| 1–3 | 1 |
| 2–3 | 2 |
| 2–4 | 5 |
| 3–4 | 3 |
| 3–5 | 6 |
| 4–5 | 7 |
Task:
- Use Kruskal’s Algorithm to find the MST.
- List the selected edges in order.
- What is the total cost of the MST?
Question 3
Graph:
| Edge | Weight |
|---|---|
| P–Q | 2 |
| Q–R | 3 |
| R–S | 6 |
| S–T | 2 |
| T–U | 4 |
| U–P | 5 |
| Q–T | 1 |
Task:
- Apply Kruskal’s Algorithm.
- Identify the cycle detection steps.
- Compute the final MST weight.
Question 4
Graph:
| Edge | Weight |
|---|---|
| 1–2 | 10 |
| 1–3 | 20 |
| 2–3 | 5 |
| 3–4 | 15 |
| 2–4 | 8 |
Task:
- Apply Kruskal’s Algorithm to find MST.
- Show sorted edge list and which edges are selected.
- Calculate total MST weight.
Question 5 (Challenge)
Graph:
| Edge | Weight |
|---|---|
| A–B | 3 |
| A–C | 1 |
| B–C | 7 |
| B–D | 5 |
| C–D | 4 |
| C–E | 2 |
| D–E | 6 |
| D–F | 8 |
| E–F | 9 |
Task:
- Apply Kruskal’s Algorithm and draw the resulting MST.
- Explain each step of Union and cycle detection.
- Compute total weight of MST.
