Separate Chaining Collision Technique

It is to keep a list of all elements that hash to the same value. An alternative to open addressing as a method of collision resolution is separate chaining hashing.

This uses an array as the primary hash table, except that the array is an array of lists of entries, each list initially being empty.

If in a set of elements, if an element hashes to the same value as that of an already inserted element then we have a collision and we need to resolve it.

In separate chaining ,each slot of the bucket array is a pointer to a linked list that contains key-value pairs that are hashed to the same location. It is otherwise called as direct chaining or simply chaining.

To handle the collision,

• This technique creates a linked list to the slot for which collision occurs.
• The new key is then inserted in the linked list.
• These linked lists to the slots appear like chains.
• That is why, this technique is called as separate chaining.

Example: Separate Chaining

Using the hash function ‘key mod 7’, insert the following sequence of keys in the hash table.

50, 700, 76, 85, 92, 73 and 101

Step-1

Draw an empty hash table.

• For the given hash function, the possible range of hash value is [0, 6].
• So, draw an empty hash table consisting of 7 buckets as below.

Step-2

Insert the given keys in the hash table one by one.

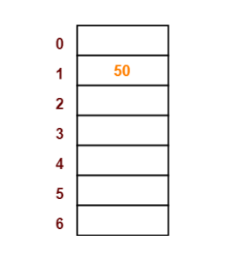
• The first key to be inserted in the hash table = 50.
• Bucket of the hash table to which key 50 maps = 50 mod 7 = 1.
• So, key 50 will be inserted in bucket-1 of the hash table as below.

Step-3

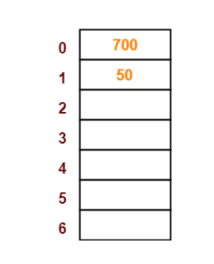
The next key to be inserted in the hash table = 700.

• Bucket of the hash table to which key 700 maps = 700 mod 7=0.
• So, key 700 will be inserted in bucket-0 of the hash table as below.

Step-4

The next key to be inserted in the hash table = 76.

• Bucket of the hash table to which key 76 maps = 76 mod 7 = 6.
• So, key 76 will be inserted in bucket-6 of the hash table as below.

Step-5

The next key to be inserted in the hash table = 85.

• Bucket of the hash table to which key 85 maps = 85 mod 7 = 1.
• Since bucket-1 is already occupied, so collision occurs.
• Separate chaining handles the collision by creating a linked list to bucket-1.
• So, key 85 will be inserted in bucket-1 of the hash table as below.

Step-6

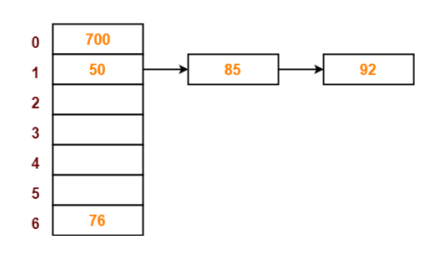
The next key to be inserted in the hash table = 92.

• Bucket of the hash table to which key 92 maps = 92 mod 7 = 1.
• Since bucket-1 is already occupied, so collision occurs.
• Separate chaining handles the collision by creating a linked list to bucket-1.
• So, key 92 will be inserted in bucket-1 of the hash table as below. Step-7

Step-7

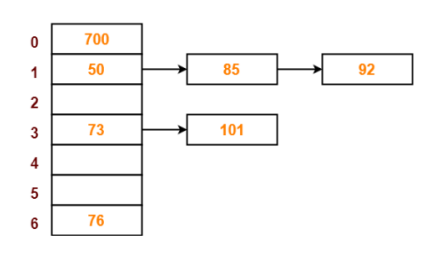
The next key to be inserted in the hash table = 101.

• Bucket of the hash table to which key 101 maps = 101 mod 7 =3.
• Since bucket-3 is already occupied, so collision occurs.
• Separate chaining handles the collision by creating a linked list to bucket-3.
• So, key 101 will be inserted in bucket-3 of the hash table as below.

Advantages

• Separate chaining is used when memory space is a concern.
• It can be very easily implemented.

Disadvantages

• It requires pointers which causes the algorithm to slow down a bit.
• Unevenly distributed keys-long lists-search time increases.

Numerical Questions of Separate Chaining Collision Technique

1. A hash table has m=10 slots and uses the hash function h(k) = k mod  10. Insert the following keys using separate chaining 12,44,13,88,23,94,11,39,20,16. Draw the hash table after all keys have been inserted.
2. Given a hash table of size m=7, and the following keys 50,700,76,85,92,73,101. Using the hash function h(k)=k mod  7, calculate the total number of collisions that occur when using separate chaining.
3. Consider a hash table of size m=9, with the hash function h(k)=k mod  9. Keys 18,41,22,44,59,32 are inserted using separate chaining.
   • Find the chain where key 59 is located.
   • How many comparisons are required to search for 59?