B-Tree

A B-Tree is a self-balancing search tree commonly used in databases and file systems to store large amounts of sorted data.

It allows search, insertion, deletion, and sequential access in logarithmic time. Unlike binary search trees (BSTs), B-Trees are optimized for systems that read and write large blocks of data.

A B-Tree is a generalized binary search tree where each node can have more than two children. It is structured to minimize disk I/O by keeping data balanced and shallow (low height).

Why B-Trees?

Binary Search Trees can become unbalanced, leading to O(n) operations.

B-Trees ensure logarithmic time complexity and are optimized for disk-based storage by storing multiple keys in a node, reducing access times.

Properties of B-Tree (of Order m)

Let’s consider a B-Tree of order m (also called degree m). This means:

• Maximum children a node can have = m
• Minimum children (except root) = ⌈m/2⌉
• Maximum keys in a node = m – 1
• Minimum keys (except root) = ⌈m/2⌉ – 1
• All leaves are at the same level.
• Keys within a node are sorted in ascending order.
• Each internal node of the B-Tree will separate its children with keys that act as dividers, ensuring that
  • All keys in the left subtree < the divider key
  • All keys in the right subtree > the divider key

Operation in B-Tree

Here's a complete explanation of all the operations in a B-Tree, including Search, Insertion, Deletion, and supporting operations like Split, Merge, and Redistribute. Each operation is designed to maintain the B-Tree's balanced structure and properties.

Search Operation

The search operation in a B-Tree is similar to binary search, but adapted for multiple keys in each node. The process begins from the root and follows the correct child pointers recursively.

• At each node:
  • Search linearly (or binary search) through keys.
  • If the key is found, return success.
  • If the key is less than a key, follow the left child pointer.
  • If the key is greater, continue to next key until the correct pointer is identified.
• If the node is a leaf and the key is not found, return failure.
• The process continues recursively until the key is found or a leaf node is reached.

Time Complexity: O(log n), because the tree is height-balanced.

Insertion Operation in B-Tree

Insertion starts by locating the correct leaf node where the new key should go. If the node is not full, we insert it in sorted order.

If the node is full (i.e., contains m - 1 keys), we need to split it. The middle key is moved up to the parent, and the node is split into two children.

Steps:

• Traverse from the root to the appropriate leaf.
• If any node on the path is full, split it before descending.
• After reaching a non-full leaf, insert the key in the correct sorted position.

If the root is full:

• A new root is created.
• The old root is split, and the tree height increases by 1.

Splitting Details:

• Mid key moves to the parent.
• Left half stays in the node.
• Right half becomes a new child.

Time Complexity: O(log n)

Deletion Operation in B-Tree

Deletion is more complex and involves several cases to maintain the tree's balance. The operation ensures that no node ends up with fewer than t - 1 keys.

There are three major scenarios:

1. Key is in a leaf node:
   • Directly delete the key if it doesn't violate the minimum keys rule.
2. Key is in an internal node:
   • If left child has ≥ t keys, replace the key with its predecessor and delete recursively.
   • If right child has ≥ t keys, replace with successor and delete recursively.
   • If both children have t - 1 keys, merge them with the key and delete recursively in the merged node.
3. Key is not in the current node:
   • Before descending, ensure the child has at least t keys.
   • If the child has only t - 1 keys:
   • Try redistribution (borrow from sibling).
   • If redistribution is not possible, perform merge with sibling.
   • Continue deletion recursively.

Time Complexity: O(log n)

Split Operation (During Insertion)

Split is triggered when a node becomes full.

How it works:

• Find the median key.
• Promote it to the parent.
• Split the node into two: left and right parts.
• If the parent is full, recursively split it too.
• If the root splits, a new root is created.

Helps keep the tree balanced and prevents overflow.

Merge Operation (During Deletion)

Merge is used when both a node and its sibling have only t - 1 keys and cannot redistribute.

How it works:

• Pull a key from the parent.
• Merge it with the underflowing node and its sibling.
• This reduces the number of keys in the parent.
• If the parent becomes empty and was the root, the tree's height decreases.

Prevents underflow but may lead to height reduction.

Redistribution / Borrow Operation (During Deletion)

Redistribution is used when a sibling has extra keys.

How it works:

• Borrow a key from the sibling.
• Move a key from the parent down to the underflowing node.
• Move a key from sibling up to parent.
• Adjust child pointers if needed.

Keeps the tree balanced without merging nodes.

Example: B-Tree of Order 3

This means:

• A node can have 2 keys at most.
• A node can have 3 children at most.
• Minimum keys (except root) = ⌈3/2⌉ – 1 = 1

Inserting: 10, 20, 5, 6, 12, 30, 7, 17

Step-by-step:

• Insert 10 → root = [10]
• Insert 20 → root = [10, 20]
• Insert 5 → root = [5, 10, 20] → node is full → split
• After split:

    [10]
   /    \
 [5]   [20]

• Insert 6 → goes to left child: [5] → becomes [5, 6]
• Insert 12 → goes to right child: [20] → becomes [12, 20]
• Insert 30 → [12, 20] → becomes [12, 20, 30] → split
• After split:

     [10, 20]
    /   |    \
  [5,6] [12] [30]

• Insert 7 → goes to [5, 6] → becomes [5, 6, 7] → split
• After split:

     [6, 10, 20]
    /   |  |   \
 [5]  [7]  [12] [30]

• Insert 17 → goes to [12] → becomes [12, 17]
• Final B-Tree:

     [6,10,20]
    /  |   |   \
 [5] [7] [12,17] [30]

Advantages of B-Tree

B-Trees are widely used in databases and file systems due to their balanced structure and efficient disk access pattern.

1. Balanced Tree Structure

B-Trees remain balanced automatically through insertions and deletions. All leaf nodes are at the same level, ensuring consistent search time.

2. Efficient Disk Read/Write

B-Trees are optimized for systems that read and write large blocks of data. Fewer disk accesses are needed due to high branching factor.

3. Supports Dynamic Growth

B-Trees adjust their structure as data is inserted or deleted. There is no need to know the number of keys in advance.

4. Logarithmic Time Complexity

Search, insert, and delete operations all have O(log n) complexity. This is true even for very large data sets.

5. High Fan-Out (Branching Factor)

Each node can have many children, which reduces tree height. Lower tree height means fewer node accesses per operation.

6. Well-Suited for Databases and File Systems

Used in indexing large amounts of data (e.g., MySQL, PostgreSQL, NTFS). Efficient for range queries and ordered traversal.

Disadvantages of B-Tree

While B-Trees are powerful, they do have some limitations and drawbacks.

1. Complex Implementation

B-Tree operations (especially deletion and balancing) are more complex to implement compared to simpler trees like binary search trees.

2. High Memory Usage

Each node stores multiple keys and multiple child pointers. This can lead to increased memory usage, especially for small data.

3. Slower than Binary Search Tree in Memory

If all data fits in memory, a binary search tree or AVL tree may perform better due to simpler structure and pointer manipulation.

4. Node Splitting and Merging Overhead

Frequent insertions and deletions can cause many node splits and merges. This may add some performance overhead during updates.

5. Less Effective for Small Datasets

For small or simple datasets, a B-Tree is overkill. Other structures like arrays, linked lists, or binary trees may be more efficient.

Note: special case for splitting the root omitted for brevity.

Example: Insert 1 to 10 numbers with t=2

Min keys possible=t-1 i.e 1

Max keys possible=2t-1 i.e 3

Maximum number of children is =2t =4

Minimum number of children is =Min key +1 =2

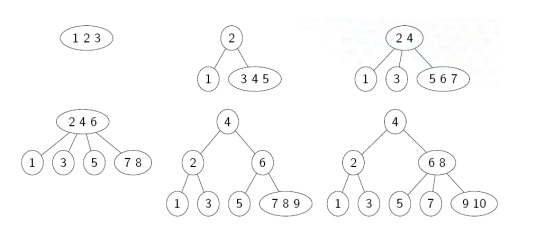
Note: if there are even number of keys so split either go for left bias or right bias. You can choose one bias for entire procedure(you can not use both biasing on entire procedure).

Deleting

• Deletion from a B-tree is a bit more complicated than insertion because a key may be deleted from any node, not just a leaf. Deletion from an internal node requires that the node's children be rearranged.

• Just as we had to ensure that nodes didn't get too big due to insertion, we have to ensure that nodes don't get too small (fewer than t -1 keys) due to deletion.

• This is done by ensuring that, before a key is deleted from a node, that node has atleast t keys |{ which may mean that we have to move an extra key into a node before we can delete anything from the node. There are two ways of moving in an extra node {| we may borrow a key from a nearby node that has more than it needs, or if we can't borrow then we may merge two nodes that have no keys to spare.

• To delete key k, we search from the root for the node containing k, and strengthen each node we visit on the way if it has fewer than t keys.

There are 3 cases for deleting from a B-tree. We reach these cases via recursion. As we recurse down the tree, we are checking which of the conditions we are in and recursively calling delete as necessary. Assume we have reached node x:

1. x is a leaf node and contains the target key to be deleted. 1.1.Leaf node contain at least t keys(more than min no. key) then simply delete that key form node.

1. Leaf node contain min number of keys then 3 subcases:
2. Barrow from left sibling if that sibling contain more than min number of keys.
3. Barrow from right sibling if that sibling contain more than min number of keys.
4. Neither left nor right sibling contain more than min keys then merge both the siblings with parent.

2. x is an internal node and contains the target key. There are 3 sub-cases:

1. predecessor child node has at least t keys(more than min no. of keys)
2. successor child node has at least t keys (more than min no. of keys)
3. Neither predecessor nor successor child has t keys (min no. of keys) then merge the both the predecessor and successor node with parent then delete.

Case 1.1 - delete 8

The node contain target key (i.e. 8) have more than min no. of keys so we can simply delete 8.

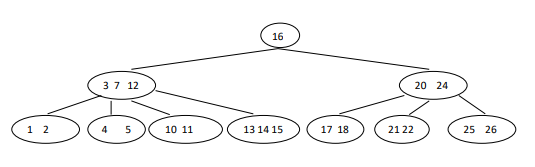
Case 1.2.2 - delete 10

The node contain key 10 contain min no. of keys so we cannot simple delete it. So barrow key from sibling node (right or left) which has more than min no of keys (right sibling node have 3 keys which more than min keys(2)).

Case 1.2.1 will be same as case 1.2.2 you have to barrow from left sibling by moving max key of left sibling to parent node and parent key to target node and then delete target key.

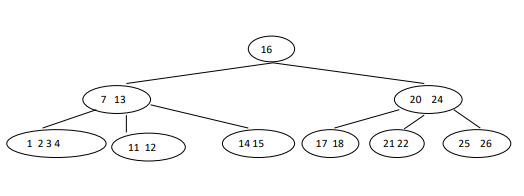
Case 1.2.3: delete 5

In this case both left and right siblings contain min no of keys, so we cannot barrow from either of them. Both the above case fails then we can merge target node with either with left or right sibling along with parent key then we can delete target key.

Case 2.1 delete 7(target key is in internal node) In this case we replace the key with its in order predecessor because predecessor node have more the min no. of key, and recursively delete the predecessor: (i.e. 4)

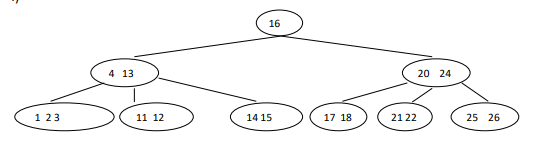
Case 2.2 similar to case 2.1

In this case we replace the key with its in order predecessor, and recursively delete the predecessor

Case 2.3 delete 20 In this case both predecessor node and successor node have min no. of keys so we can no replace with either of them. In 3 case we merge the both the predecessor and successor node along with target key. Then delete target key