Graph Data Structure

A Graph is a collection of objects where some pairs of the objects are connected by links. The objects are called vertices or nodes, and the links are called edges or arcs.

A graph G is defined as G = (V, E)

where,

• V = set of vertices (or nodes)
• E = set of edges (connections between nodes)

Example: Graph G can be defined as G = ( V , E ) Where V = {A, B, C, D, E} and E = {(A,B), (A,C), (A,D), (B,D), (C,D), (B,E), (E,D)}.

This is a graph with 5 vertices and 6 edges.

Graph is a non linear data structure. A map is a well-known example of a graph.

In a map various connections are made between the cities. The cities are connected via roads, railway lines and aerial network.

We can assume that the graph is the interconnection of cities by roads.

Euler used graph theory to solve Seven Bridges of Konigsberg problem. Is there a possible way to traverse every bridge exactly once – Euler Tour

Graph Terminology

Vertex (Node)

• A vertex is a fundamental unit of a graph, representing an entity or a point.
• Example: In a social network, each person is a vertex.
• Vertices are often labeled or numbered for identification.

Edge (Arc)

• An edge is a connection between two vertices.
• In an undirected graph, an edge is a two-way link, connecting vertex A and vertex B mutually.
• In a directed graph (digraph), an edge has a direction, represented as (u → v).
• Edges can be:
  • Unweighted: Only presence or absence matters.
  • Weighted: Each edge has a value (weight, cost, distance, capacity).

Degree of a Vertex

The degree of a vertex is the number of edges connected to it.

For Undirected Graphs:

• Degree = Number of edges incident on the vertex.
• Example: Vertex v connected to vertices a,b,c has degree 3.

For Directed Graphs:

• In-degree: Number of edges coming into the vertex.
• Out-degree: Number of edges going out from the vertex.

Example: If vertex v has 2 incoming edges and 3 outgoing edges,

• In-degree = 2
• Out-degree = 3

Adjacent Vertices (Neighbors)

• Two vertices are adjacent if they are connected directly by an edge.
• The neighbors of a vertex are all vertices adjacent to it.
• Example: In an undirected graph, if (v, w) is an edge, then v and w are neighbors.

Path

• A path is a sequence of vertices where each consecutive pair is connected by an edge.
• The length of a path is the number of edges in the path.
• Example: Path v1 → v2→ v3 →v4 has length 3.

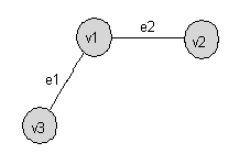
Simple Path

• A path that does not repeat vertices.
• Important in avoiding cycles.

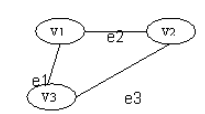
Cycle (Circuit)

• A path where the first and last vertices are the same.
• The cycle length is the number of edges involved.
• Example: v1 → v2 → v3 → v1 forms a cycle of length 3.

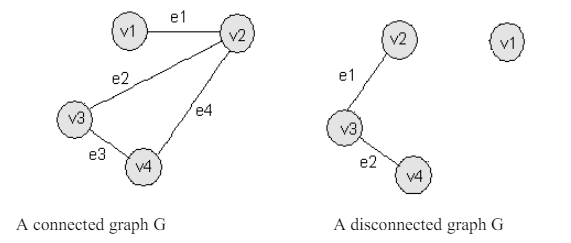
Connected Graph

• In an undirected graph, a graph is connected if there exists a path between every pair of vertices.
• If not, the graph is disconnected and has multiple connected components.

Strongly Connected Graph (Directed Graphs)

• A directed graph is strongly connected if for every pair of vertices u and v, there is a path from u to v and from v to u.

Weakly Connected Graph (Directed Graphs)

• A directed graph is weakly connected if its underlying undirected graph is connected.
• This means ignoring edge directions, the graph is connected.

Subgraph

• A graph G′ = (V′, E′) where V′ ⊆ V and E′ ⊆ E.
• Essentially a smaller graph contained within a larger graph.

Weighted Edge

• An edge that has a numerical value (weight).
• Used to represent costs, distances, or capacities.
• Example: In a road network, the weight can be the distance between cities.

Self-Loop

• An edge that connects a vertex to itself.
• Can exist in some graphs, usually avoided in simple graphs.

Multiple Edges (Parallel Edges)

• When two vertices are connected by more than one edge.
• Allowed in multigraphs, not in simple graphs.

Complete Graph

• A graph where every pair of distinct vertices is connected by a unique edge.
• Number of edges in an undirected complete graph with n vertices is: n (n − 1) / 2

Bipartite Graph

• A graph whose vertices can be divided into two disjoint sets U and V, such that every edge connects a vertex in U to one in V.
• No edges between vertices in the same set.

Tree

• A connected acyclic undirected graph.
• Has n vertices and n−1 edges.
• Special type of graph with hierarchical structure.

Degree Sequence

• The list of degrees of all vertices in a graph.
• Used to analyze graph properties.

Bridge (Cut-edge)

• An edge which, when removed, increases the number of connected components.
• It disconnects the graph.