Tree Data Structure

A tree is a widely used non-linear data structure that mimics a hierarchical tree like model, with a root and branches of connected nodes.

Unlike arrays, linked lists, stacks, or queues (which are linear), trees allow data to be organised in a parent-child relationship, making them ideal for representing hierarchies, file systems, and more.

Why Are Trees Important?

Trees are incredibly versatile:

• Efficient searching (especially with BSTs)
• Hierarchical data representation (filesystems, org charts)
• Fast insertions/deletions (compared to arrays)
• Supporting algorithms (parsing expressions, AI decision trees)

Properties of Trees

• There is one and only one path between every pair of vertices in a tree.
• A tree with n vertices has n-1 edges.
• A graph is a tree if and if only if it is minimally connected.
• Any connected graph with n vertices and n-1 edges is a tree.

Tree Terminologies

Node

• A node is an entity that contains a key or value and pointers to its child nodes.
• The last nodes of each path are called leaf nodes or external nodes that do not contain a link/pointer to child nodes.
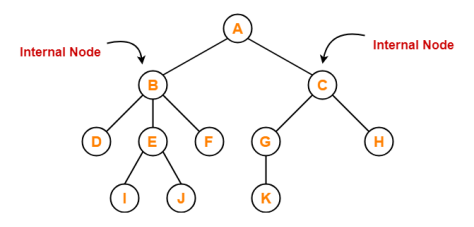
• The node having at least a child node is called an internal node.

Root

• The first node from where the tree originates is called as a root node.
• In any tree, there must be only one root node.
• We can never have multiple root nodes in a tree data structure.

Edge

• The connecting link between any two nodes is called as an edge.
• In a tree with n number of nodes, there are exactly (n-1) number of edges.

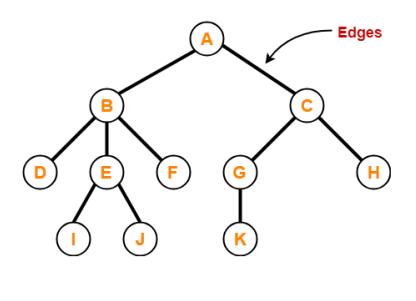
Parent

• The node which has a branch from it to any other node is called as a parent node.
• In other words, the node which has one or more children is called as a parent node.
• In a tree, a parent node can have any number of child nodes.

Child

• The node which is a descendant of some node is called as a child node.
• All the nodes except root node are child nodes.

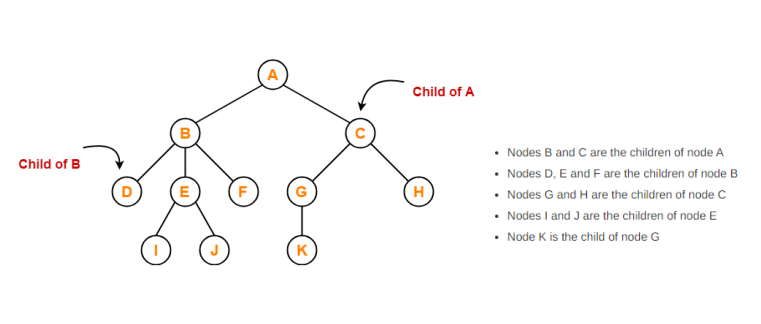
Siblings

• Nodes which belong to the same parent are called as siblings.
• In other words, nodes with the same parent are sibling nodes.

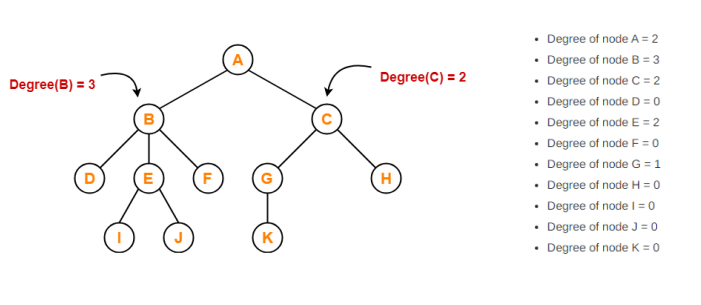
Degree

• Degree of a node is the total number of children of that node.
• Degree of a tree is the highest degree of a node among all the nodes in the tree.

Internal Node

• The node which has at least one child is called as an internal node.
• Internal nodes are also called as non-terminal nodes.
• Every non-leaf node is an internal node.

Leaf Node

• The node which does not have any child is called as a leaf node.
• Leaf nodes are also called as external nodes or terminal nodes.

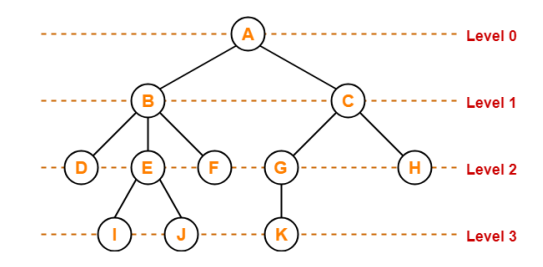
Level

• In a tree, each step from top to bottom is called as level of a tree.
• The level count starts with 0 and increments by 1 at each level or step.

Height

• Total number of edges that lies on the longest path from any leaf node to a particular node is called as height of that node.
• Height of a tree is the height of root node.
• Height of all leaf nodes = 0

Depth

• Total number of edges from root node to a particular node is called as depth of that node.
• Depth of a tree is the total number of edges from root node to a leaf node in the longest path.
• Depth of the root node = 0
• The terms “level” and “depth” are used interchangeably.

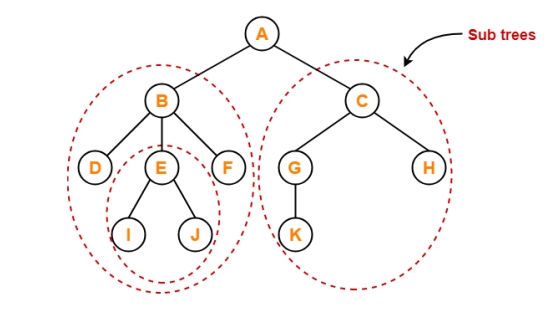
Sub Tree

• In a tree, each child from a node forms a sub-tree recursively.
• Every child node forms a sub-tree on its parent node.

Forest

A forest is a set of disjoint trees. In the given tree we remove its node then it becomes forest.

Common Operations on Trees

• Insertion (add a node)
• Deletion (remove a node)
• Traversal (visit nodes in specific order)
  • Pre-order
  • In-order
  • Post-order
  • Level-order
• Searching (find a node with a specific value)
• Finding height/depth
• Balancing (for performance)

Types of Tree

1. General Tree
2. Binary Tree: Each node has at most two children (left and right).
3. Binary Search Tree (BST): A binary tree where the left subtree contains smaller values and the right subtree contains larger values.
4. Adelson-Velsky and Landis (AVL) Tree
5. Red-Black Tree
6. N-ary Tree: Each node can have up to N children.