Priority Queue
A priority queue is a data structure where each element has a priority, and elements are always removed based on highest priority first, not just by insertion order.
If two elements have the same priority, they follow the normal FIFO (First-In-First-Out) rule.
We can implement a priority queue using:
- Arrays (simple but slower for delete)
- Linked lists
- Heaps (for better performance)
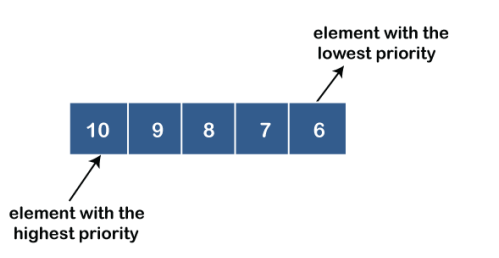
Representation of Priority Queue
Presently, we will perceive how to address the need line through a single direction list.
We will make the need line by utilizing the rundown given underneath in which INFO list contains the information components, PRN list contains the need quantities of every information component accessible in the INFO rundown, and LINK essentially contains the location of the following hub.

Let's create the priority queue step by step.
In the case of priority queue, lower priority number is considered the higher priority, i.e., lower priority number = higher priority.

Types of Priority Queue
There are two types of priority queue.
1. Ascending order Priority Queue
In rising request need line, a lower need number is given as a higher need in a need.
For instance, we take the numbers from 1 to 5 orchestrated in a rising request like 1, 2, 3, 4, 5 in this manner, the most modest number 1 is given as the most noteworthy need in a need line.

2. Descending Order Priority Queue
In plunging request need line, a higher need number is given as a higher need in a need.
For instance, we take the numbers from 1 to 5 orchestrated in diving request like 5, 4, 3, 2, 1 along these lines, the biggest number is 5 given as the most elevated need in a need line.
Operations of Priority Queue
1. Enqueue
This operation adds a new element along with its priority to the queue.
We simply store the new value at the next available position in the array and store its priority in a parallel priority array.
No sorting or reordering is done at this point we only care about priorities when removing elements.
Algorithm
Enqueue(queue[], priority[], value, p, n, size)
if n == size then
print "Queue is full"
return
end if
queue[n] ← value
priority[n] ← p
n ← n + 12. Dequeue (Remove Highest Priority Element)
This operation removes the element with the highest priority from the queue.
- Scan through the priority array to find the maximum priority.
- Identify the position (index) of this element.
- Remove the element by shifting all later elements forward by one position (so the queue stays compact).
Algorithm
Dequeue(queue[], priority[], n)
if n == 0 then
print "Queue is empty"
return
end if
max ← priority[0]
pos ← 0
for i ← 1 to n-1 do
if priority[i] > max then
max ← priority[i]
pos ← i
end if
end for
for i ← pos to n-2 do
queue[i] ← queue[i+1]
priority[i] ← priority[i+1]
end for
n ← n - 13. Peek (View Highest Priority Element)
This operation allows you to see the element with the highest priority without removing it.
We scan the priority array to find the maximum, just like in delete but we do not shift or remove anything.
Algorithm
Peek(queue[], priority[], n)
if n == 0 then
print "Queue is empty"
return
end if
max ← priority[0]
pos ← 0
for i ← 1 to n-1 do
if priority[i] > max then
max ← priority[i]
pos ← i
end if
end for
print "Highest priority element:", queue[pos]4. isEmpty
This operation checks if the queue has no elements.
We do this by checking if the count n (number of elements) is zero.
Algorithm
if n == 0 then
return True
else
return False
end if5. isFull
This operation checks if the queue has reached its maximum capacity.
We do this by comparing the current count n with the maximum allowed size size.
Algorithm
if n == size then
return True
else
return False
end ifTime and Space Complexity of Priority Queue
A priority queue is an abstract data type where each element has a priority, and the element with the highest (or lowest) priority is served first.
Depending on how you implement the priority queue, the time and space complexities will change. Let’s explore the most common cases.
Common Implementations
| Implementation Type | Description |
|---|---|
| Unsorted array/list | Insert elements anywhere; find/remove the highest-priority item by scanning. |
| Sorted array/list | Keep elements sorted by priority; fast to remove the highest, but slow to insert. |
| Binary heap | Tree-based structure (complete binary tree); most commonly used for balance between speed and simplicity. |
| Fibonacci heap (advanced) | Specialized structure with excellent amortized performance; used in advanced algorithms like Dijkstra’s or Prim’s. |
Time Complexity
| Operation | Unsorted Array/List | Sorted Array/List | Binary Heap | Fibonacci Heap |
|---|---|---|---|---|
| Insert | O(1) | O(n) | O(log n) | O(1) (amortized) |
| Delete Max/Min | O(n) | O(1) | O(log n) | O(log n) |
| Peek (Max/Min) | O(n) | O(1) | O(1) | O(1) |
| isEmpty / isFull | O(1) | O(1) | O(1) | O(1) |
Space Complexity
Regardless of implementation, the space complexity is typically.
| Component | Space |
|---|---|
| Element storage | O(n) — all stored elements |
| Auxiliary structures | O(1) or O(n) depending on implementation (heaps may use additional tree pointers) |
Overall Space Complexity: O(n) This means the space grows linearly with the number of elements you store.
Priority Queue Implementation in C Programming
#include <stdio.h>
#define SIZE 100
int data[SIZE]; // Stores values
int priority[SIZE]; // Stores priorities
int n = 0;
// Enqueue - insert based on priority
void enqueue(int value, int prio) {
if (n == SIZE) {
printf("Priority Queue is full!\n");
return;
}
int i = n - 1;
// Find the correct position based on priority (descending)
while (i >= 0 && priority[i] < prio) {
data[i + 1] = data[i];
priority[i + 1] = priority[i];
i--;
}
data[i + 1] = value;
priority[i + 1] = prio;
n++;
printf("Enqueued: value=%d, priority=%d\n", value, prio);
}
// Peek - return value with highest priority
int peek() {
if (n == 0) {
printf("Priority Queue is empty!\n");
return -1;
}
return data[0]; // Highest priority value is at index 0
}
// Dequeue - remove highest priority element
void dequeue() {
if (n == 0) {
printf("Priority Queue is empty!\n");
return;
}
printf("Dequeued: value=%d, priority=%d\n", data[0], priority[0]);
for (int i = 1; i < n; i++) {
data[i - 1] = data[i];
priority[i - 1] = priority[i];
}
n--;
}
// Display the queue
void display() {
if (n == 0) {
printf("Priority Queue is empty!\n");
return;
}
printf("Priority Queue:\n");
for (int i = 0; i < n; i++) {
printf(" Value: %d, Priority: %d\n", data[i], priority[i]);
}
}
// Main demo
int main() {
enqueue(30, 2);
enqueue(50, 4);
enqueue(20, 1);
enqueue(40, 3);
display();
printf("Peek (highest priority value): %d\n", peek());
dequeue();
display();
return 0;
}Output
Enqueued: value=30, priority=2
Enqueued: value=50, priority=4
Enqueued: value=20, priority=1
Enqueued: value=40, priority=3
Priority Queue:
Value: 50, Priority: 4
Value: 40, Priority: 3
Value: 30, Priority: 2
Value: 20, Priority: 1
Peek (highest priority value): 50
Dequeued: value=50, priority=4
Priority Queue:
Value: 40, Priority: 3
Value: 30, Priority: 2
Value: 20, Priority: 1int data[SIZE]→ stores the actual values (e.g., 30, 50, etc.)int priority[SIZE]→ stores corresponding priority values
We'll sort the elements based on priority (descending), and shift both arrays accordingly during insertion.
